Data Assimilation – The Social Metwork

Preparing for the assimilation of future ocean-current measurements

November 29, 2024The Social MetworkLeave a comment

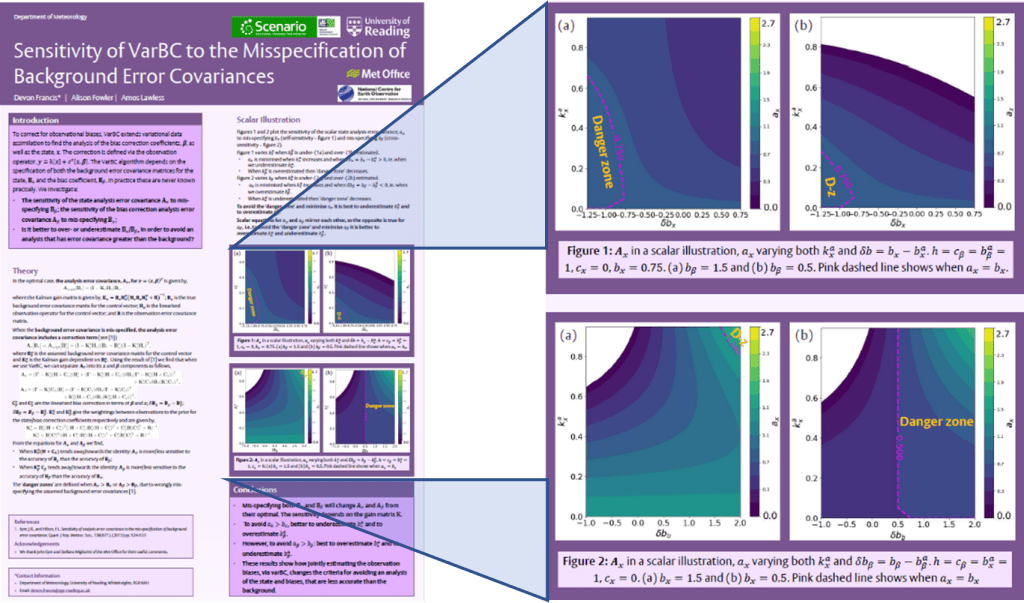
By Laura Risley

Ocean data assimilation (DA) is vital. Firstly, it is essential to improving forecasts of ocean variables. Not only that, the interaction between the ocean and atmosphere is key to numerical weather prediction (NWP) as coupled ocean-atmosphere DA schemes are used operationally.

At present, observations of the ocean currents are not assimilated operationally. This is all set to change, as satellites are being proposed to measure these ocean currents directly. Unfortunately, the operational DA systems are not yet equipped to handle these observations due to some of the assumptions made about the velocities. In my work, we propose the use of alternative velocity variables to prepare for these future ocean current measurements. These will reduce the number of assumptions made about the velocities and is expected to improve the NWP forecasts.

What is DA?

DA combines observations and a numerical model to give a best estimate of the state of our system – which we call our analysis. This will lead to a better forecast. To quote my lunchtime seminar ‘Everything is better with DA!’.

Our model state usually comes from a prior estimate which we refer to as the background. A key component of data assimilation is that the errors present in both sets of data are taken into consideration. These uncertainties are represented by covariance matrices.

I am particularly interested in variational data assimilation, which formulates the DA problem into a least squares problem. Within variational data assimilation the analysis is performed with a set of variables that differ from the original model variables, called the control variables. After the analysis is found in this new control space, there is a transformation back to the model space. What is the purpose of this transformation? The control variables are chosen such that they can be assumed approximately uncorrelated, reducing the complexity of the data assimilation problem.

Velocity variables in the ocean

My work is focused on the treatment of the velocities in NEMOVAR. This is the data assimilation software used by the NEMO ocean model, used operationally at the Met Office and ECMWF. In NEMOVAR the velocities are transformed to their unbalanced components, and these are then used as control variables. The unbalanced components of the velocities are highly correlated, therefore contradicting the assumption made about control variables. This would result in suboptimal assimilation of future surface current measurements – therefore we seek alternative velocity control variables.

The alternative velocity control variables we propose for NEMOVAR are unbalanced streamfunction and velocity potential. This would involve transforming the current control variables, the unbalanced velocities, to these alternative variables using Helmholtz Theorem. This splits a velocity field into its nondivergent (streamfunction) and irrotational (velocity potential) parts. These parts have been suggested by Daley (1993) as more suitable control variables than the velocities themselves.

Numerical Implications of alternative variables

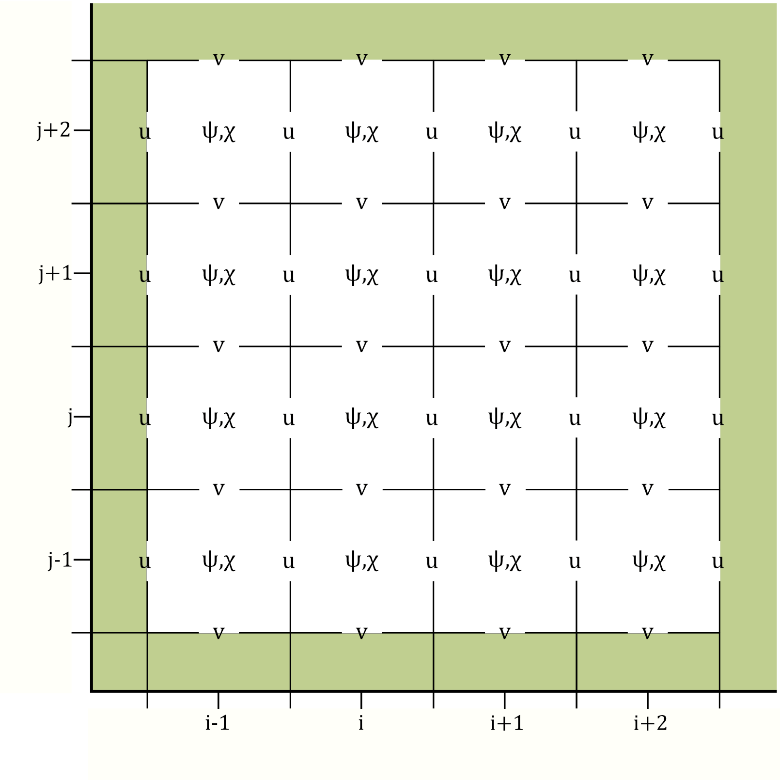
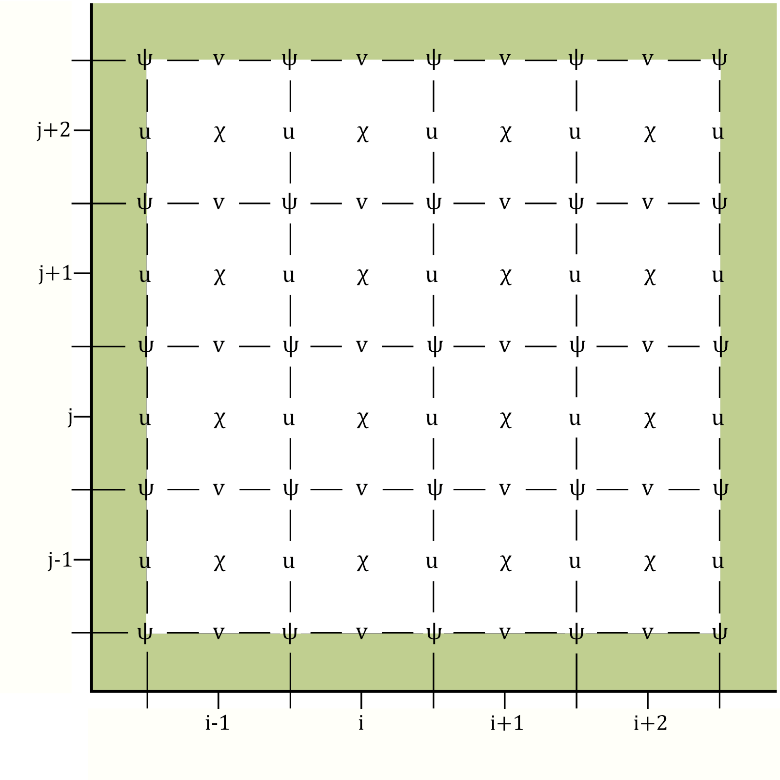
We have performed the transformation to these proposed control variables using the shallow water equations (SWEs) on a 𝛽-plane. To do so we discretised the variables on the Arakawa-C grid. The traditional placement of streamfunction on this grid causes issues with the boundary conditions. Therefore, Li et al. (2006) proposed placing streamfunction in the centre of the grid, as shown in Figure 1. This circumvents the need to impose explicit boundary conditions on streamfunction. However, using this grid configuration leads to numerical issues when transforming from the unbalanced velocities to unbalanced streamfunction and velocity potential. We have analysed these theoretically and here we show some numerical results.

Figure 1: The left figure shows the traditional Arakawa-C configuration (Lynch (1989), Watterson (2001)) whereby streamfunction is in the corner of each grid cell. The right figure shows the Arakawa-C configuration proposed by Li et al. (2006) where streamfunction is in the centre of the grid cell. The green shaded region represents land.

Issue 1: The checkerboard effect

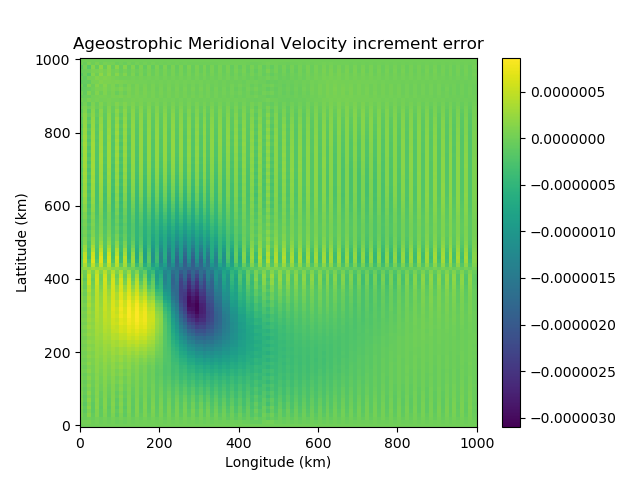
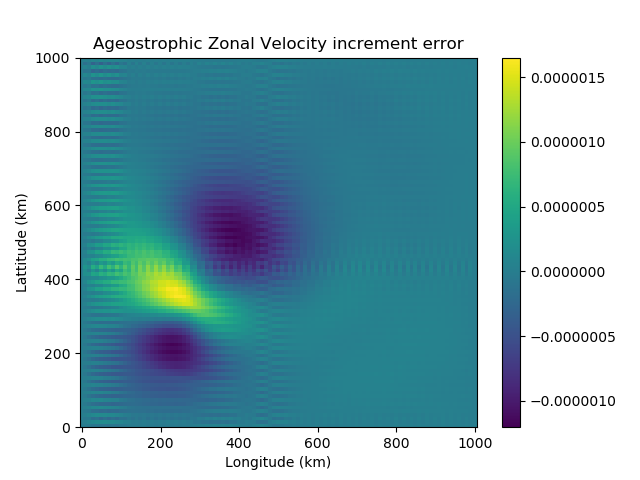
The transformation from the unbalanced velocities to unbalanced streamfunction and velocity potential involves averaging derivatives, due to the location of streamfunction in the grid cell. This process causes a checkerboard effect – whereby we have numerical noise entering the variable fields due to a loss of information. This is clear to see numerically using the SWEs. We use the shallow water model to generate a velocity field. This is transformed to its unbalanced components and then to unbalanced streamfunction and velocity potential. Using Helmholtz Theorem, the unbalanced velocities are reconstructed. Figure 2 shows the checkboard effect clearly in the velocity error.

Figure 2: The difference between the original ageostrophic velocity increments, calculated using the SWEs, and the reconstructed ageostrophic velocity increments. These are reconstructed using Helmholtz Theorem, from the ageostrophic streamfunction and velocity potential increments. On the left we have the zonal velocity increment error and on the right the meridional velocity increment error.

Issue 2: Challenges in satisfying the Helmholtz Theorem

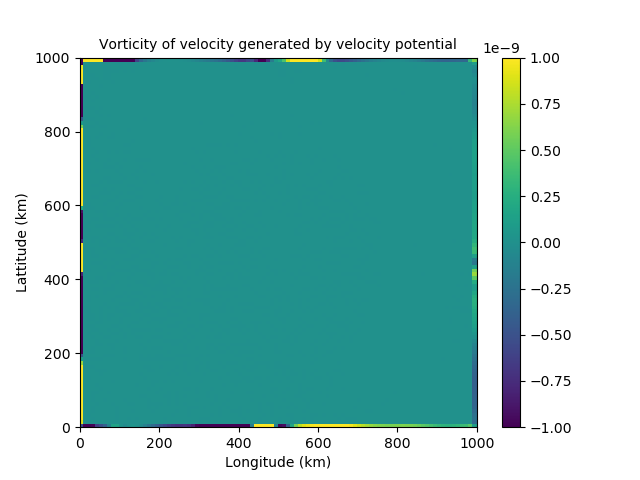
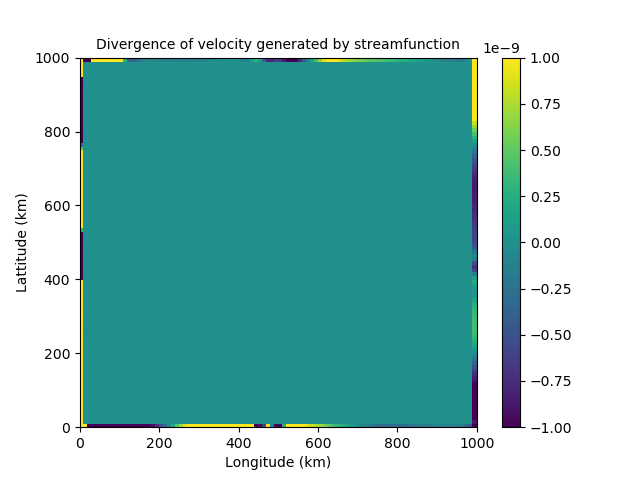
Helmholtz theorem splits the velocity into its nondivergent and irrotational components. We discovered that although streamfunction should be nondivergent and velocity potential should be irrotational, this is not the case at the boundaries, as can be seen in figure 3. This implies the proposed control variables are able to influence each other on the boundary. This would lead to them being strongly coupled and therefore correlated near the boundaries. This directly conflicts the assumption made that our control variables are uncorrelated.

Figure 3: Issues with Helmholtz Theorem near the boundaries. The left shows the divergence of the velocity field generated by streamfunction. The right shows the vorticity of the velocity field generated by velocity potential.

Overall, in my work we propose the use of alternative velocity control variables in NEMOVAR, namely unbalanced streamfunction and velocity potential. The use of these variables however leads to several numerical issues that we have identified and discussed. A paper on this work is in preparation, where we discuss some of the potential solutions. Our next work will further this investigation to a more complex domain and assess our proposed control variables in assimilation experiments.

References:

Daley, R. (1993) Atmospheric data analysis. No. 2. Cambridge university press.

Li, Z., Chao, Y. and McWilliams, J. C. (2006) Computation of the streamfunction and velocity potential for limited and irregular domains. Monthly weather review, 134, 3384–3394.

Lynch, P. (1989) Partitioning the wind in a limited domain. Monthly weather review, 117, 1492–1500.

Watterson, I. (2001) Decomposition of global ocean currents using a simple iterative method. Journal of Atmospheric and Oceanic Technology, 18, 691–703

International symposium of data assimilation 2023

November 10, 2023The Social MetworkLeave a comment

Laura Risley – l.risley@pgr.reading.ac.uk

The 9th international symposium of data assimilation (ISDA) was held in Bologna, Italy this October. Firstly, what is data assimilation? Data assimilation is the process of combining observed data with a numerical model. It also considers the errors present in both and produces the best estimate of the current state of the system. Data assimilation is used in various fields such as ocean modelling and numerical weather prediction. As such it has become an extremely important technique with high impact. ISDA is one of the largest gatherings of data assimilation scientists from across the world, and this year’s conference was no exception.

Figure 1: All talks over the course of the week were held in this room. Here is also a snippet of the schedule.

The conference took place over 5 days, each packed full of talks. There were no parallel sessions and so attendees were able to go to all 73 talks during the day! The conference didn’t stop there as there were two posters’ sessions on the Tuesday and Thursday evenings, as well as a gala dinner on the Wednesday evening which we were all invited to. This was held in the Palazzo Pepoli – the museum of the history of Bologna. A unique venue that we were fortunate enough to be able to explore before a delicious meal.

Attendees of ISDA came from various institutions. These included ECMWF, RIKEN, Penn State, The Met Office UK, CERFACS, DWD and many more. It was a truly global affair. The University of Reading was represented by members of the Data Assimilation Research Centre (DARC). Presentations were given by staff – Sarah Dance, Alison Fowler, Yumeng Chen and Ivo Pasmans, whereas PhD students presented posters – myself, Ieuan Higgs and Helen Hooker. The poster sessions were a great opportunity to discuss our work with people from various disciplines, but all interested. I found the experience extremely useful and very enjoyable, despite being quite nervous before the session. Poster sessions are a great chance to not only share your work with others but ask for advice from experts. Although it feels daunting talking to those who are far more experienced in data assimilation, you soon realise that everyone is there to learn and help each other. It is a supportive and friendly environment!

Figure 2: PhD students from DARC presenting posters at ISDA (me, Ieuan Higgs and Helen Hooker).

The conference, centred on data assimilation, covered a variety of topics from parameter estimation in earthquake models; lightning data assimilation; non-linear data assimilation and anchor observations – just to name a few! Machine learning took centre stage this year with researchers highlighting both the pitfalls and the advantages of incorporating machine learning techniques within data assimilation.

The conference has previously been held in various locations such as Reading, Munich and Fort Collins. This year it was held in Bologna, Italy and organised by Alberto Carrassi. Bologna is a wonderful city, full of historic buildings and food. Lots and lots of food. I felt very lucky to have been able to take my first trip over to Italy for the conference.

Figure 3: Some sights from Bologna!

Overall, it was a fantastic week of ensemble Kalman filters, cost functions, covariance matrices, localisation, pizza, and pasta. I learnt a lot about data assimilation; how vast the applications are and how much I still have to discover in the future. ISDA 2024 will be held in Kobe, Japan!

Ensemble Data Assimilation with auto-correlated model error

October 8, 2021October 8, 2021The Social MetworkLeave a comment

Haonan Ren – h.ren@pgr.reading.ac.uk

Data assimilation is a mathematical method to combine forecasts with observations, in order to improve the accuracy of the original forecast. Normally data assimilation methods are performed with the perfect-model assumption (weak-constraint). However, there are different sources that can produce model error, such as missing description of the dynamic system and numerical discretisation. Therefore, in recent years, the model error has been more often considered in the data assimilation process (strong-constraint settings).

There are several data assimilation methods applied in various fields. My PhD project mainly focuses on the ensemble/Monte Carlo formulation of the Kalman Filter-based methods, more specifically, the ensemble Kalman Smoother (EnKS). Different from the filter, a smoother updates the state of the system using observations from the past, present and possibly the future. The smoother does not only improve the forecast at the observation time, instead, it updates the whole simulation period.

The main purpose of my research is to investigate the performance of the data assimilation methods with auto-correlated model error. We want to know what will happen if we propose a misspecified auto-correlation in the model error, for both state update and parameter estimation. We start our project with a very simple linear auto-regressive model. As for the auto-correlation in model error, we propose an exponential decaying decorrelation. Naturally, the system has a exponential decaying parameter ω_r, and the parameter we use in the forecast and data assimilation is ω_g which can be different from the real one.

A simple example can illuminate the decorrelation issue. In Figure 1, we show results of a smoothing process for a simple one-dimensional system over a time window of 20 nature time steps. We use an ensemble Kalman Smoother with two different observation densities in time. The memories in the nature model and the forecasts models do not coincide. We can see that with ω_r = 0.0, when the actual model error is a white-in-time random variable, the evolution of the true state of the system behaves rather erratically with the present model settings. If we do not know the memory and assume the model error is a bias in the data assimilation process (ω_g → ∞), the estimation made by the data assimilation method is not even close to the truth, even with very dense observations in the simulation period, as shown in the left two subplots in Figure 1. On the other hand, if the model error in the true model evolution behaves like a bias, and we assume that the model error is white in time in the data assimilation process, the results are quite different with different observation frequencies. As shown in two subplots on the right in Figure 1, with very frequent observations, we can see a fairly good performance of the data assimilation process, but with a single observation, the estimation is still not accurate.

Figure 1: Plots of the trajectories of the true state of the system (black), three posterior ensemble members (pink, randomly chosen from 200 members), and the posterior ensemble mean (red). The left subplots show results for a true white noise model error and an assumed bias model error for two observation densities. Note that the posterior estimates are poor in both cases. The right subplots depict a bias true model error and an assumed white noise model error. The result with one observation is poor, while if many observations are present the assimilation result is consistent within the ensemble spread.

In order to evaluate the performance of the EnKS, we need to compare the root-mean-square error (RMSE) with the ensemble spread of the posterior. The best performance of the EnKS is when ratio of RMSE over the spread is equal to 1.0. The results are shown in Figure 2. As we can see, the Kalman Smoother works well when ω_g = ω_r for all the cases, with the ratio of RMSE over the spread equal to 1.0. With relatively high observational frequency, 5 observations or more in the simulation window, the RMSE is larger than the spread when ω_g > ω_r, and vice versa. In a further investigation, the mismatch between the two timescales ω_r and ω_g barely has any impact on the RMSE. The ratio is dominated by the ensemble spread.

Figure 2: Ratio of MSE over the posterior variance for the 1-dimensional system, calculated using numerical evaluation of the exact analytical expressions. The different panels show results for different numbers of observations.

Then, we move to estimating the parameter encoded in the auto-correlation of the model error. We estimate the exponential decaying parameter by the state augmentation using the EnKS, and the results are shown in Figure 3. Instead of the exponential parameter, ω_g, we use the log scale of the memory timescale to avoid negative memory estimates. The initial log-timescale values are drawn from a normal distribution: ln ω_gi ∈ N (ln ω_g, 1.0). Hence we assume that the prior distribution of the memory time scale is lognormal distributed. According to Figure 3, with an increasing number of windows we obtain better estimates. Also, the convergence is faster with more observations. And in some cases the solution did not converge to the correct value. This is not surprising given the highly nonlinear character of the parameter estimation problem, especially with only one observation per window. When we observe every time step the convergence is much faster, and the variance in the estimate decreases, as shown in the lower two subplots. In this case we always found fast convergence with different first guess and true timescale combinations, demonstrating that more observations bring us closer to the truth, and hence make the parameter estimation problem more linear.

Figure 3: PDFs of the prior (blue) and posterior (reddish colours) estimated ω_g, using an increasing number of assimilation windows. The different panels show results for different observation densities and prior mean larger (a, c) or smaller (b, d) than ω_r. The vertical black line denotes the true value ω_r.

As the results of the experiments show, the influence of an incorrect decorrelation timescale in the model error can be significant. We found that when the observation density is high, state augmentation is sufficient to obtain converging results. The new element is that online estimation is possible beyond a relatively simple bias estimate of the model error.

As a next step we will explore the influence of incorrectly specified model errors in nonlinear systems, and a more complex auto-correlation in the model error.

ECMWF/EUMETSAT NWP SAF Workshop on the treatment of random and systematic errors in satellite data assimilation for NWP

November 13, 2020November 13, 2020Devon FrancisLeave a comment

Devon Francis – d.francis@pgr.reading.ac.uk

The ECMWF/EUMETSAT NWP SAF Workshop (European Centre for Medium-Range Weather Forecasts/European Organisation for the Exploitation of Meteorological Satellites Numerical Weather Prediction Satellite Application Facilities Workshop) was originally to be held at the ECMWF centre in Reading, but as with everything else in 2020 was moved online. The workshop was designed to be a place to share new ideas and theories for dealing with errors in satellite data assimilation: encompassing the treatment of random errors; biases in observations; and biases in the model.

Group photo of attendees of ECMWF/EUMETSAT NWP SAT Workshop – Virtual Event: ECMWF/EUMETSAT NWP SAF Workshop on the treatment of random and systematic errors in satellite data assimilation for NWP.

It was held over four days: consisting of oral and poster presentations; panel discussions; and concluded on the final day with the participants split into groups to discuss what methods are currently in use and what needs to be addressed in the future.

Oral Presentations

The oral presentations were split into four sessions: scene setting talks; estimating uncertainty; correction of model and observation biases; and observation errors. The talks were held over Zoom for the main presenters and shown via a live broadcast on the workshop website. This worked well as the audience could only see the individual presenter and their slides, without having the usual worry of checking that mics and videos were off for other people in the call!

Scene Setting Talks

I found the scene setting talks by Niels Bormann (ECMWF) and Dick Dee (Joint Center for Satellite Data Assimilation – JCSDA) very useful as they gave overviews of observation errors and biases respectively: both explaining the current methods as well as the evolution of different methods over the years. Both Niels and Dick are prominent names amongst data assimilation literature, so it was interesting to hear explanations of the underlying theories from the experts in the field before moving onto the more focused talks later in the day.

Correction of Model and Observation Biases

The session about the correction of model and observation biases, was of particular interest to me as it discussed many new theoretical methods for disentangling model and observation biases which are beginning to be used in operational NWP.

The first talk by Patrick Laloyaux (ECMWF) was titled Estimation of Model Biases and Importance of Scale Separation and looked at weak-constraint 4D-Var: a variational bias correction technique that includes an error term in the model, such that solving the cost function involves varying three variables: the state; the observation bias correction coefficient; and the model error. When the background and model errors have different spatial scales and when there are sufficient reference observations, it has been shown in a simplified model that weak-constraint 4D-Var can accurately correct model and initial state errors. They argue that the background error covariance matrix contains small spatial scales, and the model error covariance matrix contains large spatial scales, which means that the errors can be disentangled in the system. However, without this scale difference, separating the errors would be much harder, so this method can only be considered when there are vast differences within the spatial scales.

On the other hand, the talk by Mark Buehner (Environment and Climate Change Canada) discussed an offline technique that performs 3D-Var analysis every six hours using only unbiased, also known as “anchor”, observations to reduce the effects of model bias. These analyses can then be used as reference states in the main 4D-EnVar assimilation cycle to estimate the bias in the radiance observations. This method was much discussed over the course of the workshop, as it is yet to be used operationally and was very interesting to see a completely different bias correction technique to tackle the problem of disentangling model and observation biases.

Posters

Poster presentations were shown via individual pages on the workshop website, with a comments section for small questions and virtual rooms – where presenters were available for a set two hours over the week. There were 12 poster presentations available, ranging from the theoretical statistics behind errors as well as operational techniques to tackle these errors.

My poster, focused on figures 1 and 2 which show the scalar state analysis error variances when (1) we vary the state background error variance accuracy for (a) underestimating and (b) overestimating the bias background error variance; (2) we vary the bias background error variance accuracy for (a) underestimating and (b) overestimating the state background error variance.

I presented a poster on work that I had been focussing on for the past few months titled Sensitivity of VarBC to the misspecification of background error covariances. My work focused on the effects of wrongly specifying the state and bias background error covariances on the analysis error covariances for the state and the bias. This was the first poster that I had ever presented so was a fast learning curve in how to clearly present detailed work in an aesthetic way. It was a useful experience as it gave me a hard deadline to conclude my current work and I had to really think about my next steps as well as why my work was important. Presenting online was a very different experience to presenting in person as it involved a lot of waiting around in a virtual room by myself, but when people did come, I was able to have some useful conversations, as well as the added bonus of being able to share my screen to share relevant papers.

Working Groups

On the final day we split ourselves into four working groups to discuss two different topics: the treatment of biases and the treatment of observation errors. The goal was to discuss current methods, as well as what we thought needed to be researched in the future or potential challenges that we would come across. This was hosted via the BlueJeans app, which provided a good space to talk as well as share screens and had the useful option to choose the ratio of viewing people’s videos, to viewing the presenter’s screen. Although I wasn’t able to contribute much, this was a really interesting day as I was able to listen to views of the experts in the field and listen to their discussions on what they believed to be the most important current issues, such as increasing discussion between data centres receiving the data and numerical weather prediction centres assimilating the data; and disentangling biases from different sources. Unfortunately for me, some of them felt that we were focussing too much on the theoretical statistics behind NWP and not enough on the operational testing, but I guess that’s experimentalists for you!

Final Thoughts

Although I was exhausted by the end of the week, the ECMWF/EUMETSAT NWP SAF Workshop was a great experience and I would love to attend next time, regardless of whether it is virtual or in person. As much as I missed the opportunity to talk to people face to face, the organisers did a wonderful job of presenting the workshop online and there were many opportunities to talk to the presenters. There were also some benefits of the virtual workshop: people from across the globe could easily join; the presentations were recorded, so can easily be re-watched (all oral and poster presentations can be found via this link – https://events.ecmwf.int/event/170/overview); and resource sharing was easy via screen sharing. I wonder whether future workshops and conferences could be a mixture of online as well as in person, in order to get the best of both worlds? I would absolutely recommend this workshop, both for people who are just starting out in DA as well as for researchers with years of experience, as it encompassed presentations from big names who have been working in error estimation for many years as well as new presenters and new ideas from worldwide speakers.

Synchronisation: how can this help weather forecasts in the future?

October 12, 2017October 12, 2017Flavia PinheiroLeave a comment

Current numerical modelling and data assimilation methods still face problems in strongly nonlinear cases, like in convective scales. A different, but interesting tool to help overcome these issues can be found in the synchronisation theory.

It all started in 1665, when Christiaan Huygens, a Dutch scientist, discovered that his two pendulum clocks were suddenly oscillating in opposite directions, but in a synchronised way. He tried to desynchronise them, by perturbing randomly one of the clocks, but surprisingly, after some time, both devices were synchronised again. He has attributed the phenomenon to the frame both clocks were sharing and after that, synchronisation field was opened to the world.

Figure 1: A drawing by Christiaan Huygens of his experiment in 1665.

Nowadays, researchers use these synchronisation concepts to reach a main goal: synchronise a model (any) with the true evolution of a system, using measurements. And even when only a reduced part of this system is observed, synchronisation between models and the true state can still be achieved. This is quite similar to what data assimilation looks for, as it aims to synchronise a model evolution with the truth by using observations, finding the best estimate of the state evolution and its uncertainty.

So why not investigate the benefits of recent synchronisation findings and combine these concepts with a data assimilation methodology?

At the start of this project, the first noticeable step that should be taken was to open up the synchronisation field to higher-dimension systems, as the experiments performed in the area were all focused on low-dimension, non-realistic systems. To this end, a first new idea was proposed: an ensemble version of a synchronisation scheme, what we are calling EnSynch (Ensemble Synchronisation). Tests with a partly observed 1000-dimension chaotic model show a very efficient correspondence between the model and the true trajectories, both for estimation and prediction periods. Figures 2 and 3 show how our estimates and the truth are on top of each other, i.e. synchronised. Note that we do not have observations for all of the variables in our system. So, it is amazing to obtain the same successful results for the observed and also for the unobserved variables in this system!

Figure 2: Trajectories of 2 variables (top:observed and bottom: unobserved). Blue lines: truth. Green lines: estimates/predictions. (Predictions start after the red lines, i.e. no data assimilation is used.)

Figure 3: Zoom in the trajectory of a variable, showing how the model matches with the truth. Blue line: truth. Red line: our model. Yellow dots: observations.

The second and main idea is to test a combination of this successful EnSynch scheme with a data assimilation method called Particle Filter. As a proper data assimilation methodology, a particle filter provides us the best estimation of the state evolution and its uncertainty. Just to illustrate the importance of data assimilation in following the truth, figure 4 compares the case of only counting on an ensemble of models running freely in a chaotic nonlinear system, with the case of a data assimilation method applied to it.

Figure 4: Trajectories of ensemble members. Blue: with data assimilation. Red: without data assimilation. Truth is in black.

Efficient results are found with the combination between the new EnSynch and the particle filters. An example is shown in figure 5, where particles (ensemble members) of an unobserved variable nicely follow the truth during the assimilation period and also during the forecast stage (after t=100).

Figure 5: Trajectory for an unobserved variable in a 1000-dimension system. Observations occur at every 10 time steps until t=100. Predictions start after t=100.

These results are motivating and the next and big step is to implement this combined system in a bigger atmospheric model. This methodology has been shown to be a promising solution for strongly nonlinear problems and potential benefits are expected for numerical weather prediction in the near future.

References:

Rey, D., M. Eldridge, M. Kostuk, H. Abarbanel, J. Schumann-Bischoff, and U. Parlitz, 2014a: Accurate state and parameter estimation in nonlinear systems with sparse observations. Physics Letters A, 378, 869-873, doi:10.1016/j.physleta.2014.01.027.

Zhu, M., P. J. van Leeuwen, and J. Amezcua, 2016: Implicit equal-weights particle filter. Quart. J. Roy. Meteorol. Soc., 142, 1904-1919, doi:10.1002/qj.2784.

Tales from the Alice Holt forest: carbon fluxes, data assimilation and fieldwork

February 24, 2017Ewan PinningtonLeave a comment

Email: ewan.pinnington@gmail.com

Forests play an important role in the global carbon cycle, removing large amounts of CO₂ from the atmosphere and thus helping to mitigate the effect of human-induced climate change. The state of the global carbon cycle in the IPCC AR5 suggests that the land surface is the most uncertain component of the global carbon cycle. The response of ecosystem carbon uptake to land use change and disturbance (e.g. fire, felling, insect outbreak) is a large component of this uncertainty. Additionally, there is much disagreement on whether forests and terrestrial ecosystems will continue to remove the same proportion of CO₂ from the atmosphere under future climate regimes. It is therefore important to improve our understanding of ecosystem carbon cycle processes in the context of a changing climate.

Here we focus on the effect on ecosystem carbon dynamics of disturbance from selective felling (thinning) at the Alice Holt research forest in Hampshire, UK. Thinning is a management practice used to improve ecosystem services or the quality of a final tree crop and is globally widespread. At Alice Holt a program of thinning was carried out in 2014 where one side of the forest was thinned and the other side left unmanaged. During thinning approximately 46% of trees were removed from the area of interest.

flux_me — Figure 1: At the top of Alice Holt flux tower.

Using the technique of eddy-covariance at flux tower sites we can produce direct measurements of the carbon fluxes in a forest ecosystem. The flux tower at Alice Holt has been producing measurements since 1999 (Wilkinson et al., 2012), a view from the flux tower is shown in Figure 1. These measurements represent the Net Ecosystem Exchange of CO₂ (NEE). The NEE is composed of both photosynthesis and respiration fluxes. The total amount of carbon removed from the atmosphere through photosynthesis is termed the Gross Primary Productivity (GPP). The Total Ecosystem Respiration (TER) is made up of autotrophic respiration (R_a) from plants and heterotrophic respiration (R_h) from soil microbes and other organisms incapable of photosynthesis. We then have, NEE = -GPP + TER, so that a negative NEE value represents removal of carbon from the atmosphere and a positive NEE value represents an input of carbon to the atmosphere. A schematic of these fluxes is shown in Figure 2.

forest_fluxes — Figure 2: Fluxes of carbon around a forest ecosystem.

The flux tower at Alice Holt is on the boundary between the thinned and unthinned forest. This allows us to partition the NEE observations between the two areas of forest using a flux footprint model (Wilkinson et al., 2016). We also conducted an extensive fieldwork campaign in 2015 to estimate the difference in structure between the thinned and unthinned forest. However, these observations are not enough alone to understand the effect of disturbance. We therefore also use mathematical models describing the carbon balance of our ecosystem, here we use the DALEC2 model of ecosystem carbon balance (Bloom and Williams, 2015). In order to find the best estimate for our system we use the mathematical technique of data assimilation in order to combine all our available observations with our prior model predictions. More infomation on the novel data assimilation techniques developed can be found in Pinnington et al., 2016. These techniques allow us to find two distinct parameter sets for the DALEC2 model corresponding to the thinned and unthinned forest. We can then inspect the model output for both areas of forest and attempt to further understand the effect of selective felling on ecosystem carbon dynamics.

In Figure 3 we show the cumulative fluxes for both the thinned and unthinned forest after disturbance in 2015. We would probably assume that removing 46% of the trees from the thinned section would reduce the amount of carbon uptake in comparison to the unthinned section. However, we can see that both forests removed a total of approximately 425 g C m^-2 in 2015, despite the thinned forest having 46% of its trees removed in the previous year. From our best modelled predictions this unchanged carbon uptake is possible due to significant reductions in TER. So, even though the thinned forest has lower GPP, its net carbon uptake is similar to the unthinned forest. Our model suggests that GPP is a main driver for TER, therefore removing a large amount of trees has significantly reduced ecosystem respiration. This result is supported by other ecological studies (Heinemeyer et al., 2012, Högberg et al., 2001, Janssens et al., 2001). This has implications for future predictions of land surface carbon uptake and whether forests will continue to sequester atmospheric CO₂ at similar rates, or if they will be limited by increased GPP leading to increased respiration.

References

Wilkinson, M. et al., 2012: Inter-annual variation of carbon uptake by a plantation oak woodland in south-eastern England. Biogeosciences, 9 (12), 5373–5389.

Wilkinson, M., et al., 2016: Effects of management thinning on CO2 exchange by a plantation oak woodland in south-eastern England. Biogeosciences, 13 (8), 2367–2378, doi: 10.5194/bg-13-2367-2016.

Bloom, A. A. and M. Williams, 2015: Constraining ecosystem carbon dynamics in a data-limited world: integrating ecological “common sense” in a model data fusion framework. Biogeosciences, 12 (5), 1299–1315, doi: 10.5194/bg-12-1299-2015.

Pinnington, E. M., et al., 2016: Investigating the role of prior and observation error correlations in improving a model forecast of forest carbon balance using four-dimensional variational data assimilation. Agricultural and Forest Meteorology, 228229, 299 – 314, doi: http://dx.doi.org/10.1016/j.agrformet.2016.07.006.

Heinemeyer, A., et al., 2012: Exploring the “overflow tap” theory: linking forest soil co2 fluxes and individual mycorrhizo- sphere components to photosynthesis. Biogeosciences, 9 (1), 79–95.

Högberg, P., et al., 2001: Large-scale forest girdling shows that current photosynthesis drives soil respiration. Nature, 411 (6839), 789–792.

Janssens, I. A., et al., 2001: Productivity overshadows temperature in determining soil and ecosystem respiration across european forests. Global Change Biology, 7 (3), 269–278, doi: 10.1046/j.1365-2486.2001.00412.x.

Continue reading →

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: